Peak Distance (Diffusion Distance)

At a particular time, the distance at which the signal amplitude is largest is the peak depth. The peak depth observed in Fig. 54 (b) can be dervied by setting the depth derivative of the analytic solution for \(E_x\) to zero. Where:

\[e_x(t>0) = E_{x,0}^- \frac{\big (\mu\sigma)^{1/2} z}{2\pi^{1/2} t^{3/2}} \, e^{-\mu\sigma z^2/4t}\]

is the quasi-static analytic solution, the peak distance is given by:

(131)\[z_{max} = \sqrt{\frac{2 t}{\mu\sigma}} \approx 1260 \sqrt{\frac{ t}{\sigma}}.\]

This quantity is frequently referred to as the diffusion distance. It acts as a time domain equivalent for the skin depth.

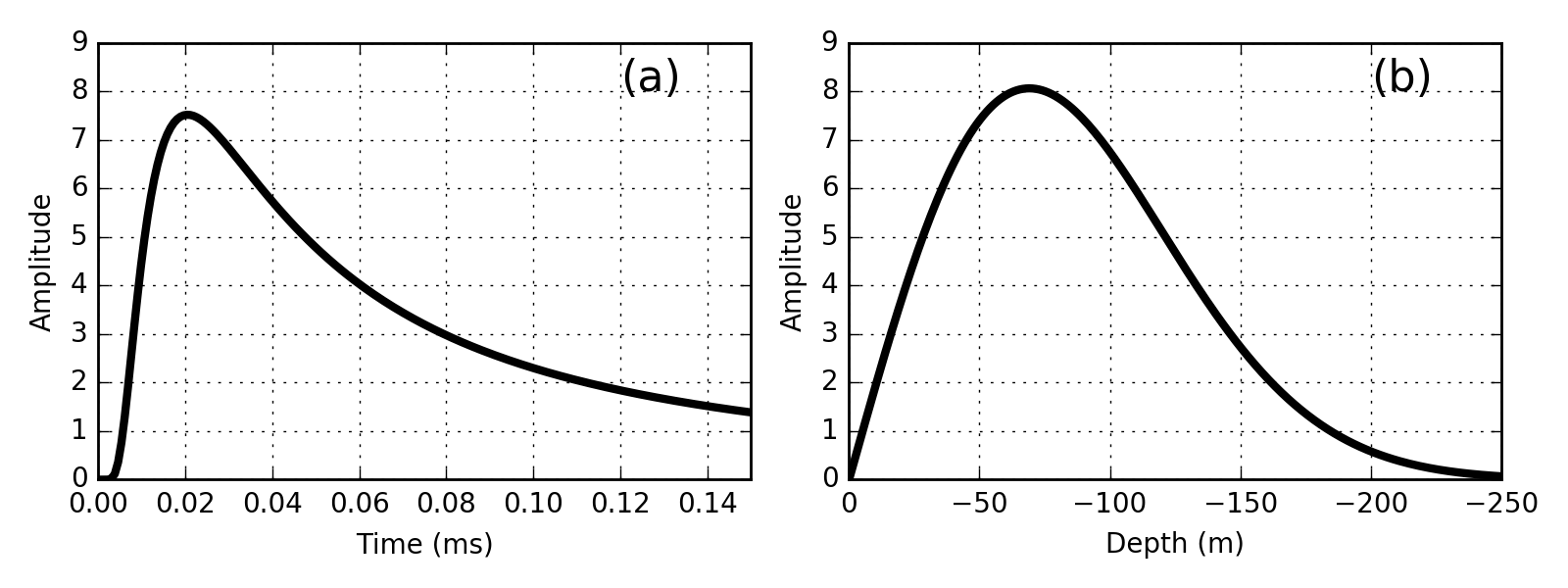
Fig. 54 Electric field as a function of time 100 m from a 1D impulse in the field in a 0.01 S/m whole space (a). Electric field at t = 0.03 ms as a function of distance (Modifed from [WH88]) (b).