Peak Time

The peak time is the time at which the maximum signal amplitude is observed at a particular location. The peak time observed in Fig. 55 (a) can be dervied by setting the time derivative of the analytic solution for \(E_x\) to zero. Where:

\[e_x(t>0) = E_{x,0}^- \frac{\big (\mu\sigma)^{1/2} z}{2\pi^{1/2} t^{3/2}} \, e^{-\mu\sigma z^2/4t}\]

is the quasi-static analytic solution, the peak time is given by:

(132)\[t_{max} = \frac{\mu\sigma z^2}{6}\]

For an impulse excitation, the peak time is proportional to the square of the distance traveled.

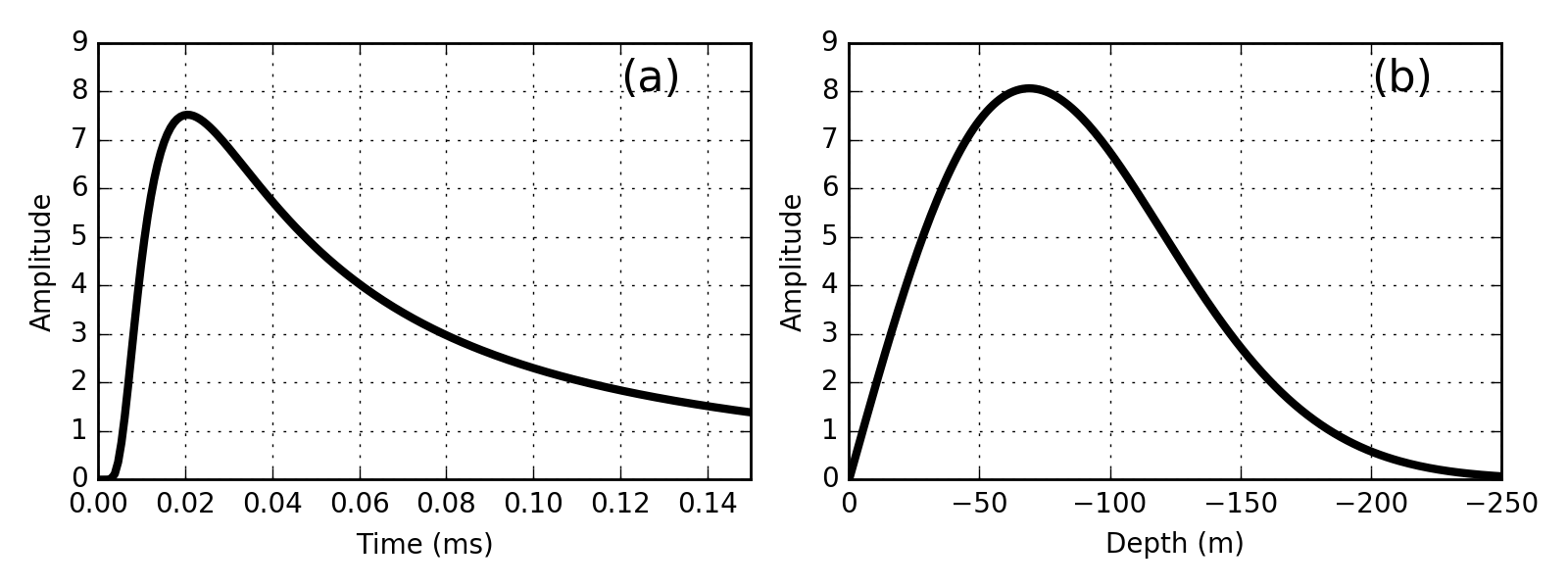
Fig. 55 Electric field as a function of time 100 m from a 1D impulse in the field in a 0.01 S/m whole space (a). Electric field at t = 0.03 ms as a function of distance (Modifed from [WH88]) (b).