Attenuation and Skin Depth

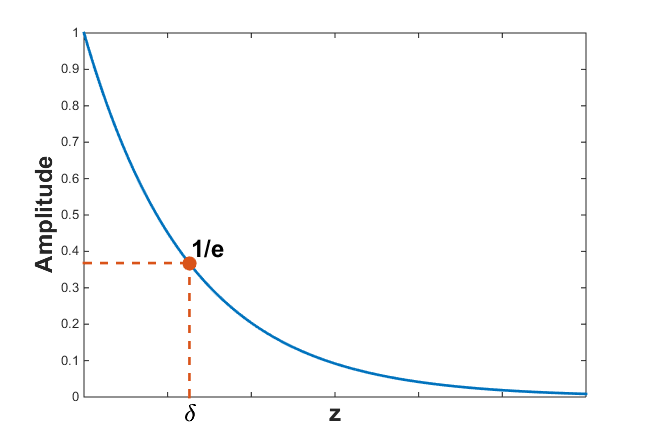
Fig. 45 Skindepth is defined as the depth at which the amplitude of the wave has been reduced by \(1/e\).

Attenuation

Attenuation defines the rate of amplitude loss an EM wave experiences at it propagates (Fig. 45). The attenuation of an EM wave is defined by the parameter \(\beta\). For a downgoing planewave, the attenuation formula is given by:

\[A(z) = A_0 e^{\beta z}\]

where absolute \(A\) is the amplitude, \(A_0\) is the absolute amplitude at \(z\) = 0 m and:

\[\beta = \omega \left ( \frac{\mu\epsilon}{2} \left [ \left ( 1 + \frac{\sigma^2}{\epsilon^2 \omega^2} \right)^{1/2} - 1 \right ] \right ) ^{1/2} \geq 0\]

Skin Depth

Skin depth defines the distance a wave must travel before its amplitude has decayed by a factor of \(1/e\). The skin depth is the reciprocal of the decay constant \(\beta\). Thus:

\[\delta = \frac{1}{\beta} = \frac{1}{\omega} \left ( \frac{\mu\epsilon}{2} \left [ \left ( 1 + \frac{\sigma^2}{\epsilon^2 \omega^2} \right)^{1/2} - 1 \right ] \right ) ^{1/2}\]

Since \(\beta\) depends on the frequency and the physical properties of the media, so does the skin depth. For a general case, the skin depth can be considered a fairly complicated function. However, approxmations exist in the quasi-static and wave regimes.

Skin Depth for Various Materials

The table below shows skin depths for certain rocks at various frequencies. This is meant to serve as a general guide, as rock types are classified by a range of physical properties values which can lead to order of magnitude differences in skin depth.

Type	\(\sigma\)	\(\mu_r\)	\(\epsilon_r\)	\(\delta\) (1Hz)	\(\delta\) (1kHz)	\(\delta\) (1MHz)	\(\delta\) (1GHz)
Air	0 S/m	1	1	\(\infty\)	\(\infty\)	\(\infty\)	\(\infty\)
Sea Water	3.3 S/m	1	80	277 m	8.76 m	0.277 m	0.015 m
Igneous	\(10^{-4}\) S/m	1	5	50,300 m	1,590 m	121 m	119 m
Sedimentary (dry)	\(10^{-3}\) S/m	1	4	15,900 m	500 m	18 m	11 m
Sedimentary (wet)	\(10^{-2}\) S/m	1	25	5,000 m	160 m	5.4 m	2.6 m
Sulphide Skarn	\(10^{2}\) S/m	1	5	50 m	1.6 m	0.05 m	0.002 m
Magnetite Skarn	\(10^{2}\) S/m	2	5	36 m	1.1 m	0.04 m	0.001 m

Approximations

Quasi-Static Approximation

In the quasi-static regime (\(\epsilon\omega \ll \sigma\)), the skin depth is approximately equal to:

\[\delta = \frac{1}{\beta} = \sqrt{\frac{2}{\omega \mu \sigma}}.\]

Assuming the Earth is non-magnetic (\(\mu = \mu_0 = 4\pi \times 10^{-7}\) H/m) and replacing \(\omega=2\pi f\), a simpler form of the skin depth is given by:

\[\delta \approx 503 \sqrt{\frac{1}{f \sigma}} = 503 \sqrt{\frac{\rho}{f}}.\]

where \(\rho = 1/\sigma\) is the resistivity. Thus from the previous two equations, we see that the skin depth decreases as the conductivity \(\sigma\), magnetic permeability \(\mu\) and frequency \(\omega\) increase. In most cases however, the magnetic properties are negligible as \(\mu \sim \mu_0\).

Wave-Regime Approximation

In the wave regime (\(\epsilon\omega \gg \sigma\)), the skin depth is approximately equal to:

\[\delta = \frac{1}{\beta} = \frac{2}{\sigma} \sqrt{\frac{\epsilon}{\mu}}\]

Assuming the Earth is non-magnetic (\(\mu = \mu_0 = 4\pi \times 10^{-7}\) H/m) and by using the relative permittivity \(\epsilon_r = \epsilon/\epsilon_0\), a simpler form of the skin depth is given by:

\[\delta \approx 0.0053 \frac{\sqrt{\epsilon_r}}{\sigma}\]

Thus from the previous two equations, we see that the skin depth decreases proportional \(\sqrt{\epsilon_r}/\sigma\); provided the magnetic properties are negligible (\(\mu \sim \mu_0\)). The below shows skin depths for some representative rocks and frequencies in the wave regime. To see how physical properties and frequencies affect skin depth, check out the app.