Biot-Savart

A bit of History

The relationship characterizing the magnetic flux generated by a electric current was first described by Jean-Baptiste Biot and Félix Savart, two French physicists. Their original experiment involved passing current through a very long vertical wire which moved magnetic some needle distance away from the wire. They built this experiment together in 1820, around the same time Ampere and Faraday were also running theirs own experiments, 4 decades before Maxwell unified electromagnetic theory. As it had not yet been discovered, this law does not take into account the second term of the Ampere-Maxwell’s law, which is time dependent.

Definition

\[\mathbf{b}= \frac{\mu_{0}}{4 \pi} \int_{C} \frac{I_{enc} \mathbf{dl} \times \mathbf{\hat{r}}} {r^2}\]

In steady state, this equation is fundamental for forward modelling the magnetic flux created by an active source such as a loop. It is closely related to the Ampere’s law.

Some examples

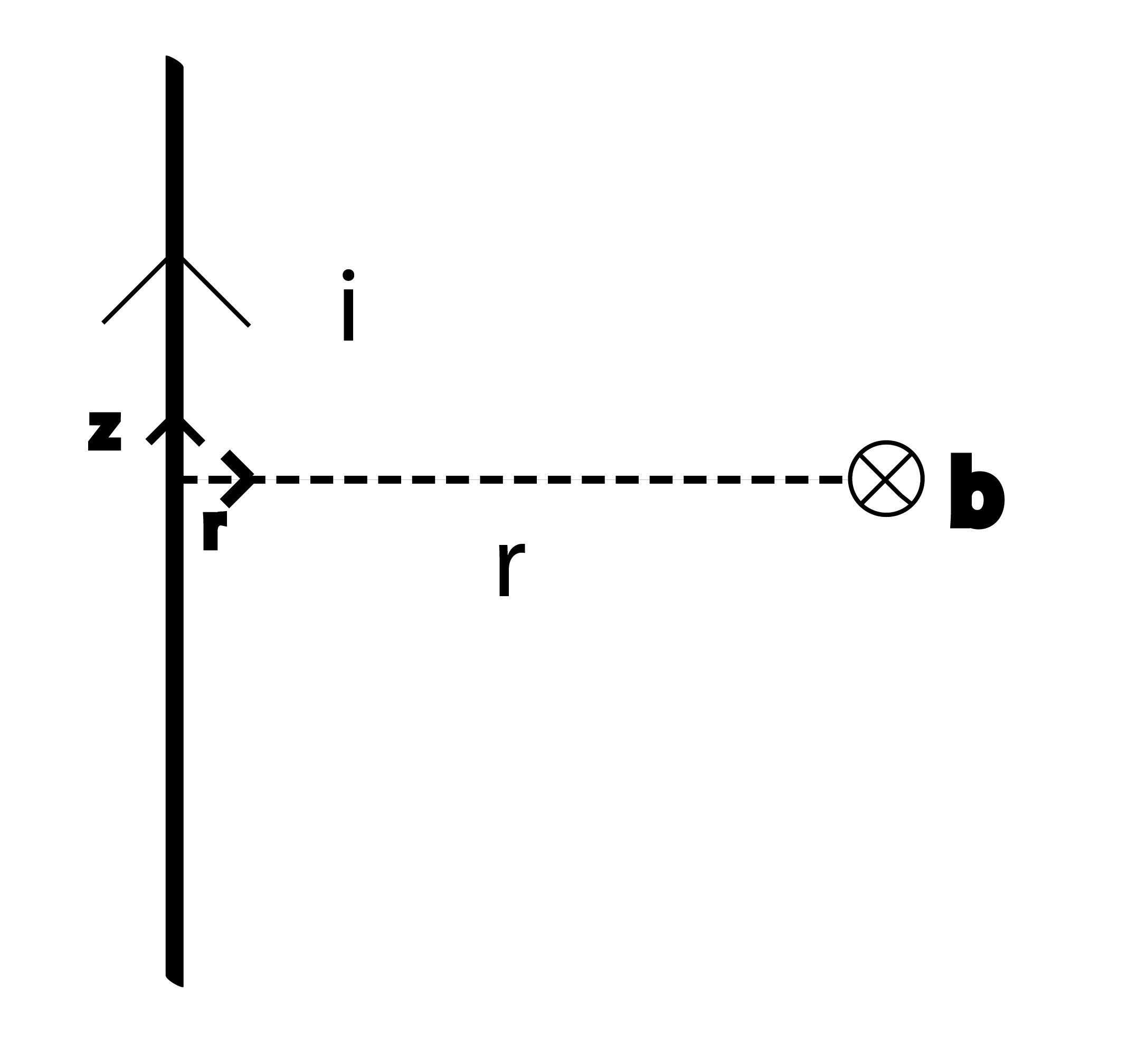
Infinite vertical wire

Given an infinite vertical wire along the axis \(\mathbf{z}\), infinitesimally thin carrying an electric current of intensity \(i\), the value of generated magnetic flux at every point in space at a distance \(r\) (with direction indicated by the unit vector \(\mathbf{\hat{r}}\)) from the wire is:

\[\mathbf{b(r)}= \frac{\mu_{0} I_{enc}}{2 \pi r } ({\mathbf{\hat{z}} \times \mathbf{\hat{r}}})\]

Magnetic flux along the central axis of a loop

Given a loop of radius \(R\), which is infinitesimally thin, carrying a electric current of intensity \(i\), the generated magnetic flux along the central axis of the loop \(\mathbf{z}\), at a distance \(r\), is:

\[\mathbf{b}= \frac{\mu_{0} I_{enc}}{2} \frac{R^2}{(r^2+R^2)^{\frac{3}{2}}} \mathbf{\hat{z}}\]

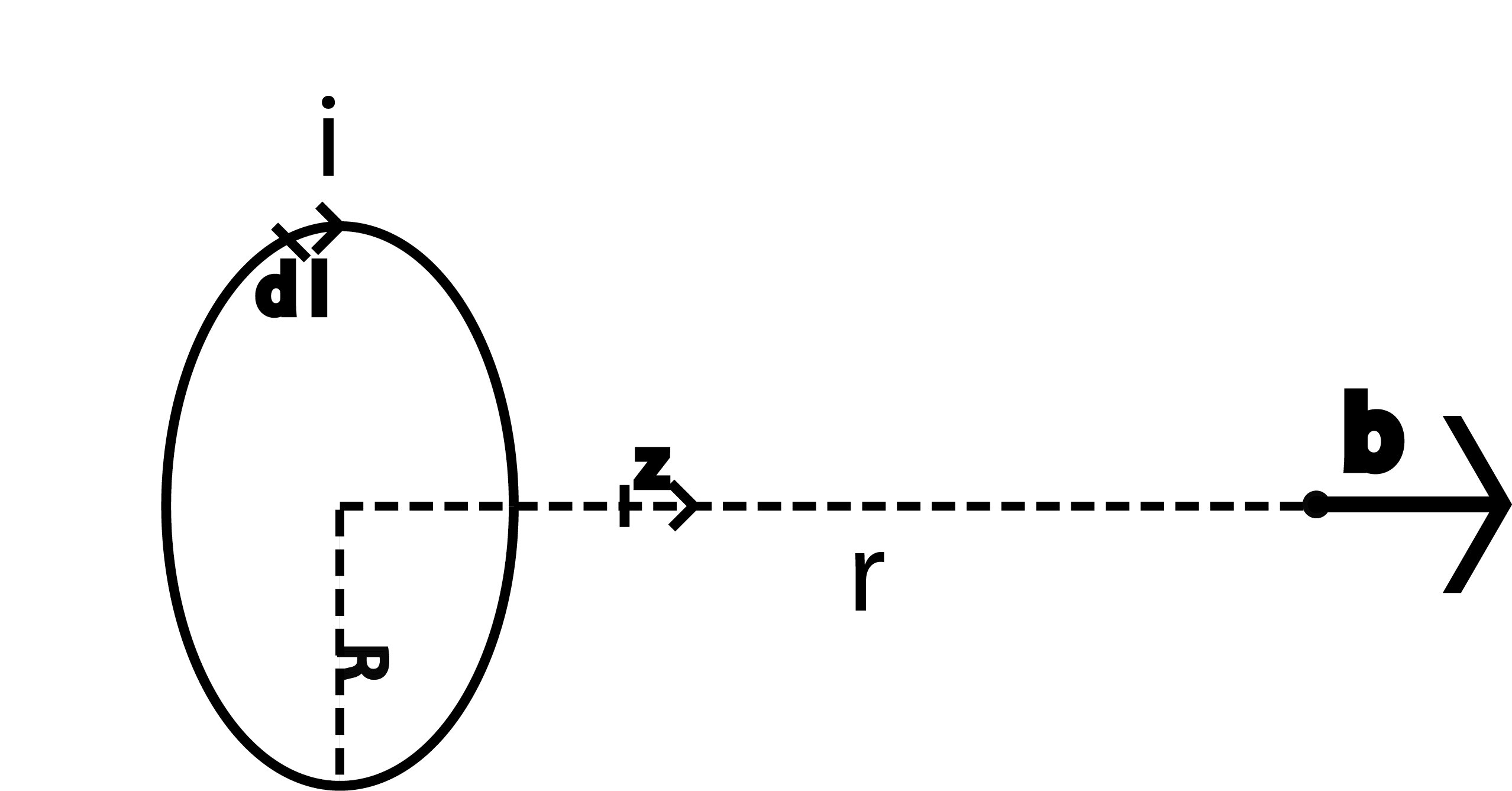
Note: Considering \(\mathbf{dl}\) and \(\mathbf{\hat{z}}\) form a direct (orthonormal system, the direction of the flux is given by the sign of \(i\) )