Interface Conditions

Charge Buildup at Boundaries

Consider the situation in the figure below, at a boundary between two media with different conductivities but both with dielectric permittivity \(\varepsilon = \varepsilon_0\).

We will show how charge buildup occurs at such an interface using conservation of charge, Ohm’s law and the interface condition on the normal component of electric displacement. Recall the integral equation expressing conservation of charge

(333)\[\int_A \mathbf{j} \cdot da = - \frac{d}{dt} \int_V \rho dv = - \frac{dQ}{dt}.\]

In steady state, \(dQ/dt = 0\). Taking the surface of integration as our standard Gaussian pillbox (see boundary conditions page), the integral can be evaluated as

(334)\[\begin{split}(\mathbf{j}_2-\mathbf{j}_1)\cdot\hat{\mathbf{n}} &= 0 \\ j_{2n} &= j_{1n}.\end{split}\]

where \(j_{1n}\) and \(j_{2n}\) are the normal components of current density on either side of the interface. So we see that direct current is continuous across material interfaces. If we assume, linear, isotropic earth materials, we can apply Ohm’s law (\(\mathbf{j}_f = \sigma\mathbf{e}\)) to this equation, yielding

(335)\[\sigma_2\mathbf{e}_{2n} = \sigma_1\mathbf{e}_{1n}.\]

Since we assume that both materials have dielectric permittivity \(\varepsilon = \varepsilon_0\), we can write the interface condition on the normal component of electric displacement in terms of the electric field

(336)\[\mathbf{e}_{2n}-\mathbf{e}_{1n}\ = \frac{\tau_f}{\varepsilon_0},\]

where \(\tau_f\) is the free surface charge density on the boundary.

combining the two previous equations we can express the charge buildup in terms of the ratio of the two conductivities

(337)\[\frac{\tau_f}{\varepsilon_0} = \Big(\frac{\sigma_1}{\sigma_2}-1\Big)\mathbf{e}_{1n}.\]

In the case where current is flowing from a resistive layer to a more conductive layer (i.e. \(\sigma_2 > \sigma_1\)),

\[\sigma_1 < \sigma_2 \implies \tau_f <0\]

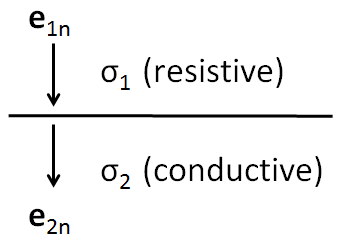
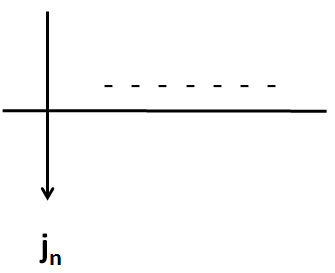
We get a buildup of negative charges on the boundary, and in the case where flow is from a resistive layer to a conductive layer (i.e. \(\sigma_1 > \sigma_2\))

\[\sigma_1 > \sigma_2 \implies \tau_f >0\]

We get a buildup of positive charges on the boundary.