Wave Impedance and Phase

Wave Impedance

Wave impedance defines the ratio between transverse components of the electric and magnetic fields supported by an EM planewave. For the downward propagating EM planewave shown in Fig. 47, the impedance is given by:

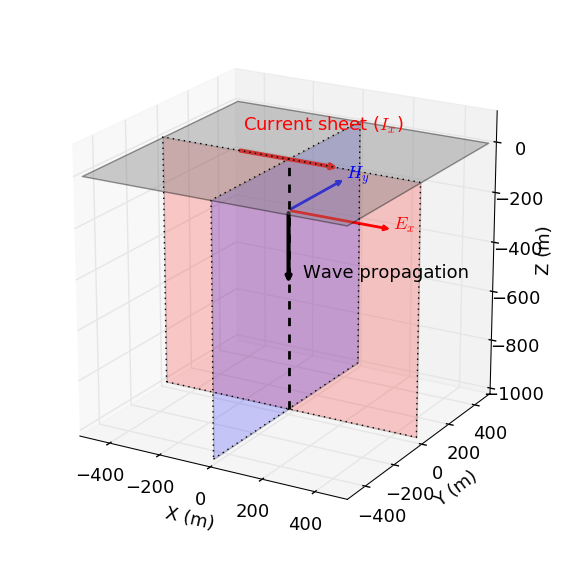
Fig. 47 Geometry of an EM planewave propagating downwards.

\[Z_{xy} = -\frac{E_x}{H_y} = \frac{\omega \mu}{k}\]

where \(\mu\) is the magnetic permeability and \(k\) is the complex wavenumber. From the previous equation, we see that the wave impedance depends on the frequency and physical properties of the medium. Thus in a homogeneous isotropic medium, a single wave impedance can be used to characterize EM waves propagating in any direction. However if the physical properties are anisotropic (direction dependent), waves propagating in different directions are characterized by separate impedances.

Phase

The wave impedance can be used to obtain the phase difference between the electric and magnetic fields supported by a planewave. The phase difference between the electric and magnetic fields shown in Fig. 47:

\[\phi_{Z_{xy}} = \textrm{tan}^{-1} \Bigg ( \frac{\textrm{Im}[Z_{xy}]}{\textrm{Re}[Z_{xy}]} \Bigg )\]

where \(0 \leq \phi_{xy} \leq \pi/4\). According the above expression, the electric field lags the magnetic field.

Approximations

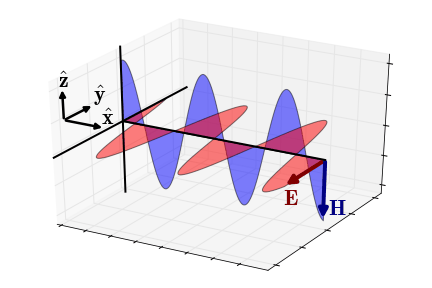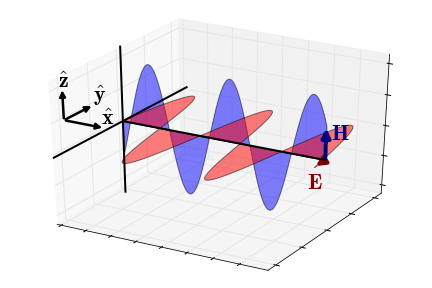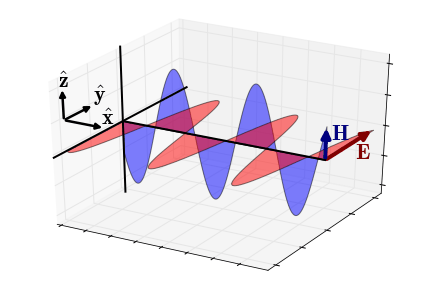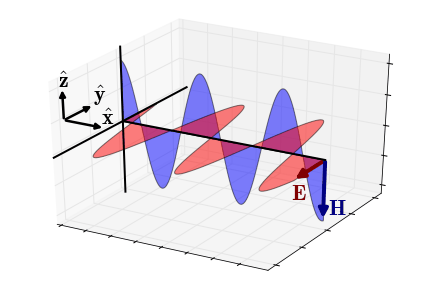
Fig. 48 Electric and magnetic fields of an EM wave propagating in the x-direction (quasi-static regime).

Quasi-Static Approximation

In the quasi-static regime (\(\epsilon \omega \ll \sigma\)), the wavenumber becomes \(\sqrt{-i\omega\mu\sigma}\) and the impedance simplifies to:

\[Z_{xy} = \frac{\omega \mu}{\sqrt{-i\omega\mu\sigma}} = \sqrt{\frac{i \omega \mu}{\sigma}}\]

The phase of the impedance is given by:

\[\phi_{Z_{xy}} = \textrm{tan}^{-1} \Bigg ( \frac{\textrm{Im}[Z_{xy}]}{\textrm{Re}[Z_{xy}]} \Bigg ) = \frac{\pi}{4}\]

In this case, the electric field lags the magnetic field by \(\pi/4\) radians.

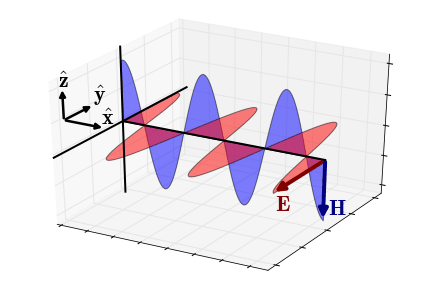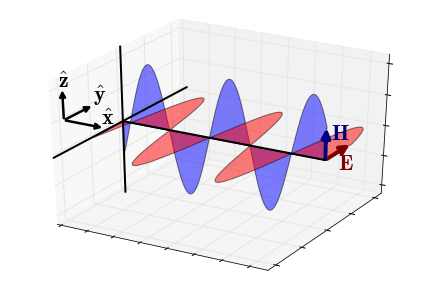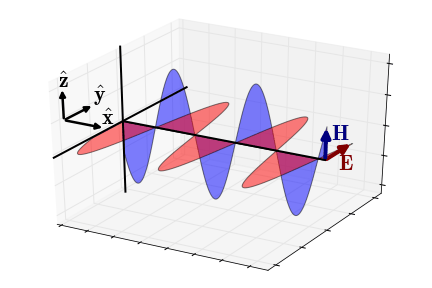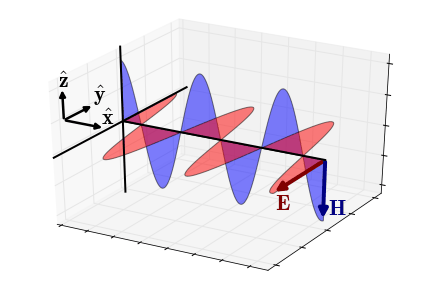
Fig. 49 Electric and magnetic fields of an EM wave propagating in the x-direction (wave regime).

Wave Regime Approximation

In the wave regime (\(\epsilon \omega \gg \sigma\)), the wavenumber simplifies to \(\omega \sqrt{\mu\epsilon}\) and the impedance simplifies to:

\[Z_{xy} = \frac{\omega \mu}{\omega \sqrt{\mu\epsilon}} = \sqrt{\frac{\mu}{\epsilon}}\]

where the phase is equal to:

\[\phi_{Z_{xy}} = \textrm{tan}^{-1} \Bigg ( \frac{\textrm{Im}[Z_{xy}]}{\textrm{Re}[Z_{xy}]} \Bigg ) = 0\]

In this case, the electric and magnetic fields are in phase with one another.