Total Reflection and Brewster’s Angle

Purpose

We first identify total reflection and brewster angle for a dielectric media, then relate them to conductive medium.

Total Reflection

For a perfect dielectric, the conductivity is zero and the permeability is that of free space that is, \(\mu_1=\mu_2=\mu_0\). In this case, Snell’s law reduces to:

(325)\[\frac{\text{sin} \theta_i}{\text{sin} \theta_t} = \frac{k_1}{k_2} = \Big(\frac{\epsilon_2}{\epsilon_1}\Big)^{1/2} = n_{12}\]

where \(n_{12}\) is the relative index of refraction. If \(\epsilon_2 > \epsilon_1\) then \(n_{12} > 1\). Under this situation, for any angle of incidence \(\theta_i\) there is a real angle of transimission \(\theta_t\). On the other hand, if \(\epsilon_2 < \epsilon_1\) then \(\theta_t\) is real only when \(n_{12} \text{sin} \theta_t \leq 1\). Total reflection occurs when \(n_{12}\text{sin} \theta_t > 1\), and indicates that the wave cannot pass through and is entirely reflected. For the reflection from a conductive surface, a total reflection occurs when \(\sigma_1 > \sigma_2\). Fig. 78 illustrate this.

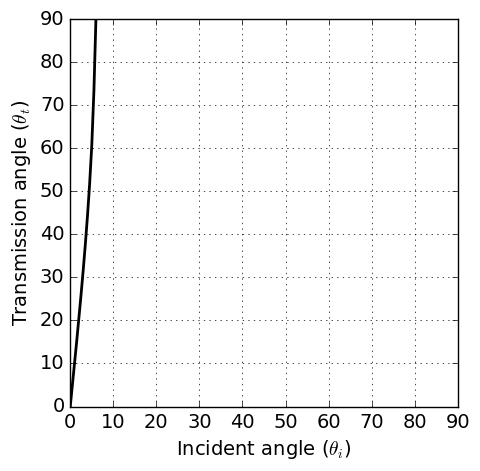
Fig. 78 Tranmission angle \(\theta_t\) as a function of the incident angle \(\theta_i\) when \(\sigma_1\) = 1 S/m and \(\sigma_2\) = 0.1 S/m. Magnetic permeability and dielectric permittivitivy assumed to be those of free-space (\(\epsilon = \epsilon_0\) and \(\mu = \mu_0\))

Brewster’s Angle

From derived reflection coefficients for TE mode in Fresnel Equations, the reflection coefficient for perfect dielectric can be written as

\[r_{TE} = \frac{(\epsilon_1)^{1/2} \text{cos} \theta_i - (\epsilon_2)^{1/2} \text{cos} \theta_t}{(\epsilon_1)^{1/2} \text{cos} \theta_i + (\epsilon_2)^{1/2} \text{cos} \theta_t}\]

With Snell’s law of refraction shown in Eq. (325), above equation can be modified as

\[r_{TE} = \frac{\text{cos} \theta_i \text {sin} \theta_t - \text{cos} \theta_t \text {sin} \theta_i}{\text{cos} \theta_i \text {sin} \theta_t + \text{cos} \theta_t \text {sin} \theta_i} = \frac{\text {sin} (\theta_t - \theta_i)}{\text {sin}(\theta_t + \theta_i)}\]

Similarly, the reflection coefficient for TM mode can be obtained as

\[r_{TM} = \frac{\text {tan} (\theta_t - \theta_i)}{\text {tan}(\theta_t + \theta_i)}\]

Power reflection coefficient for TE and TM mode can be

\[R_{TE} \equiv |r_{TE}|^2 = \frac{\text {sin}^2 (\theta_t - \theta_i)}{\text {sin}^2(\theta_t + \theta_i)}\]

\[R_{TM} \equiv |r_{TM}|^2 = \frac{\text {tan}^2 (\theta_t - \theta_i)}{\text {tan}^2(\theta_t + \theta_i)}\]

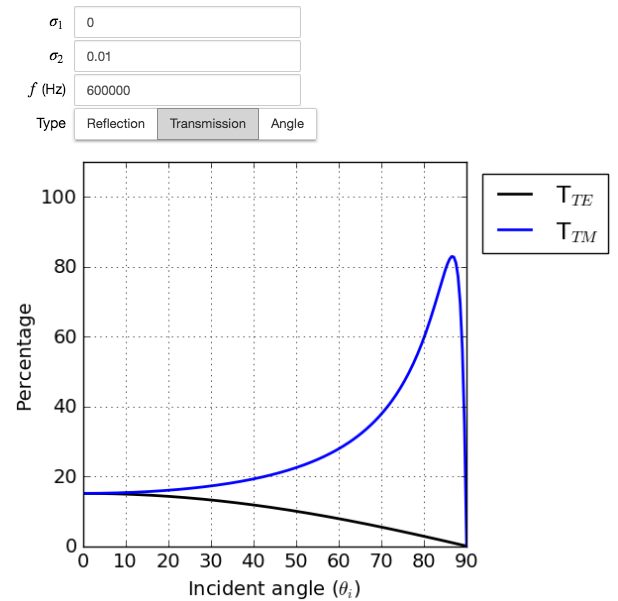
Accordingly, power transmission coefficient will be

\[T_{TE} \equiv 1-|r_{TE}|^2\]

\[T_{TM} \equiv 1-|r_{TM}|^2\]

If \((\theta_t + \theta_i) \rightarrow \pi/2\), then \(\text{tan}(\theta_t + \theta_i) \rightarrow \infty\), and \(r_{TM} \rightarrow 0\). The reflected and refracted waves are normal to one another, and

\[\text {sin} \theta_t = \text {sin} (\pi/2 - \theta_i) = \text {cos} \theta_i\]

so that Eq. (325) becomes

\[\text {tan} \theta_i = \Big(\frac{\epsilon_2}{\epsilon_1}\Big)^{1/2} = n_{12}\]

The angle that this equation satisfies is known as the Brewster angle. The reflection from a conductive surface, there will be a minimum in \(R_{TM}\), analogous to the Brewster angle, for some particular angle of incidence. No such minimul occurs in \(R_{TE}\). Fig. 79 illustrate this.

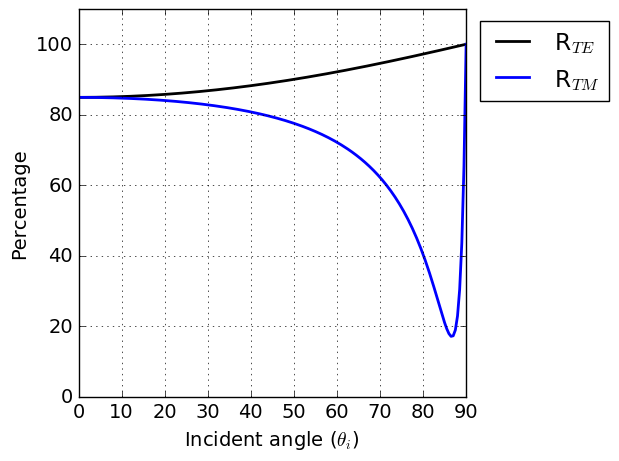
Fig. 79 The power reflection coefficient \(R_{TE}\) and \(R_{TM}\) versus angle of incidence for plane wave at air-earth interface. The conductivity and dielectric permitivity of earth are taken to be 0.01 S/m, and \(\epsilon = \epsilon_0\), respectively. The frequency is 6 x 10 ⁵ Hz.

App

Fig. 78 and Fig. 79 are generated by the Reflection and Refraction app that you can adjust conductivity of each medium, and obtain corresponding transmission angle, power reflection and transmission coefficients as a function of incident angle. Below link will direct you to the app: