Frequency-Dependent Magnetic Permeability

In response to changes in an applied magnetic field, the induced magnetization within most rocks may be considered an instantaneous process. For some lateritic soils and rapidly cooled basalts however, a portion of the induced magnetization undergoes a relaxation process. This relaxation process is commonly referred to as: viscous remanent magnetization, magnetic viscosity, or magnetic after-effect. As a result of their magnetic viscosity, lateritic soils and rapidly cooled basalts are characterized by frequency-dependent magnetic permeabilities.

Here, our description of the magnetic viscosity is limited to providing useful expressions for implementation in applied problems. Comprehensive studies of magnetic viscosity, and its relevance to geophysical surveying, may be found in ([Bus82, DJT92, Das06, DOzdemir97, Lee84, Neel49, Pas07]).

Mathematical Description

For rocks which are characterized by frequency-dependent magnetic permeabilities, the magnetic constitutive relationship becomes:

(28)\[{\bf B}(\omega) = \mu (\omega) \, {\bf H}(\omega)\]

where \(\mu (\omega)\) may also be characterized a frequency-dependent magnetic susceptibility \(\chi (\omega)\):

(29)\[\mu (\omega) = \mu_0 \big [ 1 + \chi (\omega) \, \big ]\]

As presented in magnetism in rocks, magnetic susceptibility represents the proportional degree of induced magnetization, in response to an applied magnetic field. For rocks exhibiting magnetic viscosity, the relaxation process may be understood by considering a Debye model:

(30)\[\chi(\omega) = \chi_\infty + \frac{\chi_0 - \chi_\infty}{1 + i \omega \tau}\]

where \(\chi_0\) defines the zero-frequency limit, \(\chi_\infty\) defines the infinite frequency limit, and \(\tau\) defines the rate of magnetic relaxation. The instantaneous portion of induced magnetization is represented by \(\chi_\infty\), whereas \(\chi_0-\chi_\infty\) represents the viscous contribution. In rocks, the magnetic viscosity is characterized by a distribution of time-relaxation constants. This can be represented by introducing a weighting function \(f(\tau)\), and integrating over all Debye models:

(31)\[\chi (\omega) = \chi_\infty + \big ( \chi_0 - \chi_\infty \big ) \int_0^\infty \frac{f(\tau)}{1 + i\omega\tau} d\tau\]

The magnetic viscosity of a rock ultimately depends on the distribution of time relaxation constants. From expression (31), a multitude of models have been proposed. One of the simplest and most popular models is obtained by assuming a log-uniform distribution of time relaxation constants:

(32)\[\chi(\omega) = \chi_0 - \frac{\chi_0 - \chi_\infty}{ln (\tau_2/\tau_1)} ln \Bigg ( \frac{1 + i\omega\tau_2}{1 + i\omega\tau_1} \Bigg )\]

where \(\tau_1\) and \(\tau_2\) represent lower and upper bounds for distribution. A specific weighting function may also be used to obtain the Cole-Cole model:

(33)\[\chi(\omega) = \chi_\infty + \frac{\chi_0 - \chi_\infty}{1 + (i \omega \tau_c)^\alpha}\]

where \(\tau_c\) represents the center of a distribution of time- relaxation constants, and \(\alpha\) represents the broadness of the distribution. The frequency-dependent magnetic susceptibilities for a Debye model, log-uniform distribution, and Cole-Cole model are compared in Fig. 31.

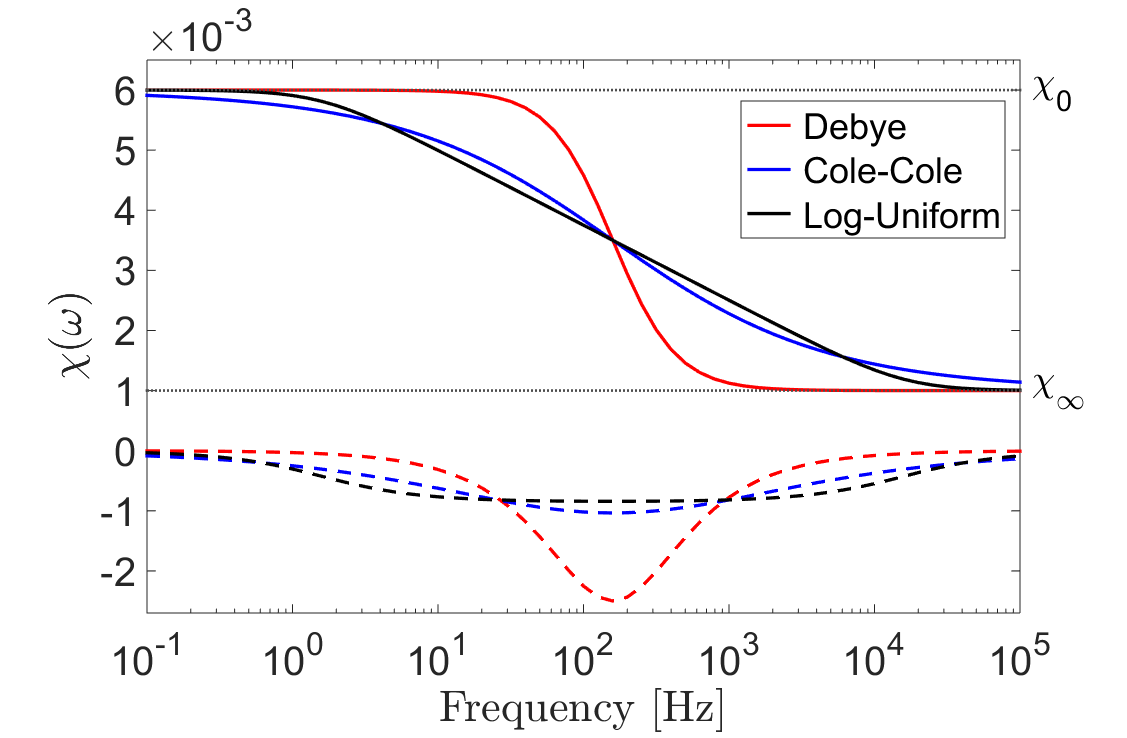
Fig. 31 Comparison between frequency-dependent magnetic susceptibilities for a Debye model (\(\chi_0=6\times 10^{-3}, \; \chi_\infty = 10^{-3}\)), a log-uniform distribution of time-relaxation constants (\(\chi_0=6\times 10^{-3}, \; \chi_\infty = 10^{-3}, \tau_1=10^{-5} \; s, \tau_2 =10^{-1} \, s\)), and a Cole-Cole model (\(\chi_0=6\times 10^{-3}, \; \chi_\infty = 10^{-3}, \tau_c = 10^{-3} \, s, \alpha = 0.5\)).